Merge Sort in Java - Algorithm Example

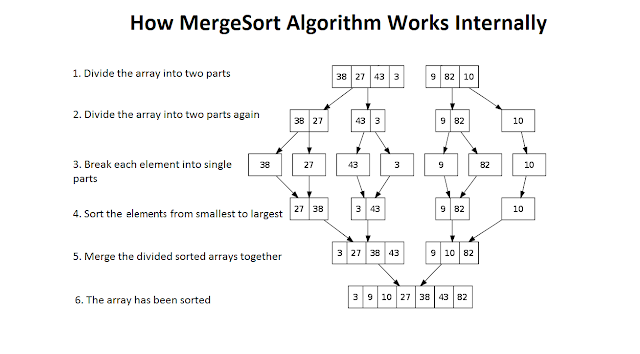
The merge sort algorithm is a divide and conquers algorithm. In the divide and conquer paradigm, a problem is broken into smaller problems where each small problem still retains all the properties of the larger problem -- except its size. To solve the original problem, each piece is solved individually; then the pieces are merged back together. For example, imagine you have to sort an array of 200 elements using the bubble sort algorithm. Since selection sort takes O(n^2) time, it would take about 40,000-time units to sort the array. Now imagine splitting the array into ten equal pieces and sorting each piece individually still using selection sort. Now it would take 400-time units to sort each piece; for a grand total of 10*400 = 4000.

Once each piece is sorted, merging them back together would take about 200-time units; for a grand total of 200+4000 = 4,200. Clearly, 4,200 is an impressive improvement over 40,000.

Now think bigger. Imagine splitting the original array into groups of two and then sorting them. In the end, it would take about 1,000-time units to sort the array.

That's how merge sort works. It makes sorting a big array easy and hence it's suitable for large integer and string arrays. Time Complexity of the mergesort algorithm is the same in the best, average and worst-case and it's equal to O(n*log(n))

Btw, if you are new to Algorithms and Data Structure and not familiar with an essential sorting and searching algorithms like quicksort, binary search, level order search etc then I suggest you go through a good, comprehensive online course like Data Structures and Algorithms: Deep Dive Using Java to learn the basics first.

Sorting Array using Merge Sort Algorithm:

You have given an unordered list of integers (or any other objects e.g. String), You have to rearrange the integers or objects in their natural order.

Sample Input: {80, 50, 30, 10, 90, 60, 0, 70, 40, 20, 5}
Sample Output: {0, 10, 20, 30, 40, 50, 50, 60, 70, 80, 90}

import java.util.Arrays;

/*
 * Java Program to sort an integer array using merge sort algorithm.
 */

public class Main {

  public static void main(String[] args) {

    System.out.println("mergesort");
    int[] input = { 87, 57, 370, 110, 90, 610, 02, 710, 140, 203, 150 };

    System.out.println("array before sorting");
    System.out.println(Arrays.toString(input));

    // sorting array using MergeSort algorithm
    mergesort(input);

    System.out.println("array after sorting using mergesort algorithm");
    System.out.println(Arrays.toString(input));

  }

  /**
   * Java function to sort given array using merge sort algorithm
   *
   * @param input
   */
  public static void mergesort(int[] input) {
    mergesort(input, 0, input.length - 1);
  }

  /**
   * A Java method to implement MergeSort algorithm using recursion
   *
   * @param input
   *          , integer array to be sorted
   * @param start
   *          index of first element in array
   * @param end
   *          index of last element in array
   */
  private static void mergesort(int[] input, int start, int end) {

    // break problem into smaller structurally identical problems
    int mid = (start + end) / 2;
    if (start < end) {
      mergesort(input, start, mid);
      mergesort(input, mid + 1, end);
    }

    // merge solved pieces to get solution to original problem
    int i = 0, first = start, last = mid + 1;
    int[] tmp = new int[end - start + 1];

    while (first <= mid && last <= end) {
      tmp[i++] = input[first] < input[last] ? input[first++] : input[last++];
    }
    while (first <= mid) {
      tmp[i++] = input[first++];
    }
    while (last <= end) {
      tmp[i++] = input[last++];
    }
    i = 0;
    while (start <= end) {
      input[start++] = tmp[i++];
    }
  }
}

Output
mergesort
array before sorting
[87, 57, 370, 110, 90, 610, 2, 710, 140, 203, 150]
array after sorting using mergesort algorithm
[2, 57, 87, 90, 110, 140, 150, 203, 370, 610, 710]

You can see that the array is now sorted. The algorithm we have used is a recursive implementation of merge sort and it's also a stable sorting algorithm I mean it maintains the original order of elements in case of a tie.

Btw, you would need a Pluralsight membership to access this course, which costs around $29 per month or $299 per year but also provides you access to all of their 5000+ online courses on the latest technologies.

That's all about how to implement the merge sort algorithm in Java. Along with Quicksort it's an important sorting algorithm and used in many real-world, general-purpose libraries. In fact, Java's Collections.sort() and Arrays.sort() method also used a variant of merge sort for soring objects.

If you are preparing for a programming job interview then you must know how to implement it by hand and find out time and space complexity. You should also be able to explain the difference between merge sort and quicksort if asked.

The key thing to remember here is that even though both merge sort and quick sort has an average case time complexity of O(NlogN), quicksort is better than merge sort because the constant associated with quicksort is lesser than merge sort.

In reality, O(NlogN) is K*O(nLogN), Big O notation ignore that constant because it gets irrelevant when input size increases exponentially but for algorithms with same time complexity, this constant could be a differentiating factor, just like it is in the case of quicksort and mergesort.

You should also remember that it's a recursive algorithm and can be easily implemented using recursion.

Source: java67.com